Hey，Neway。这里是2020年炎热的夏天。

2020年可能是你这辈子一提起都会感慨一些事的一年：噢那年啊，那个新冠可是持续了一年，我戴了一年口罩，在宿舍办公了一年；噢那年中美彻底撕破脸了；对我来说，除了这些国家大事，自己的人生也是在一个重大的转折点上，这也是我为什么想给你写封信，而不是按之前那样，碎碎念的记录日子：不知道这个转折点后的你，会在哪里，带着什么样的心情读这封信，所以也是蛮有意思的。

其实你也知道这个转折点是什么意思：今年是准备申请的一年，现在是7月20日，我也背了快2/3的单词了，但是每次复习的时候还是有很多单词不认识。教授也还没开始套瓷，感觉教授们的方向没有一个和我特别match，做GCN的没有做EDA的，做EDA的没有做GCN的。没套瓷还有另一个原因：ICCAD没中啦。

感觉写的像野马奔腾一样没有主线，那就先说说ICCAD没中这件事上。给个评价的话，算是意料之中但又出乎意料吧，意料之中是因为实验都没做完，test layout只拿了一个circuit，其他的实在是跑不完了；就这一点就足够杀掉这篇paper了。意料之外是这个work比起DAC那篇是让我满意特别多的work；是一个让我觉得自己不是一个只知道套DL SOTA的缝合怪的work；也是一个可以让我特别自豪的showoff的work。哎，所以知道没中的时候真的还是感觉好可惜呐，本来还想着iccad也直接中，就可以底气十足的抬头挺胸去套瓷了，但现在就很尴尬了，申请前我能投的paper除去这篇recycle到ASPDAC的就只有一篇target ICLR的work了，而且也没有recycle的机会了。。。哎，只能安慰自己publication并不算很重要吧。

除去对我申请的直接影响，这次没中还让我给自己一个清晰的认知：或者说是泼了一盆冷水，虽然自诩想当威斯布鲁克不想当科沃尔，但是真没中需要recycle的时候还是让我明白，我不是什么特别适合research的天才。基于此，有个最近困扰我很久的更严重的问题：所谓德不配位，我这种水平的臭弟弟，就算侥幸伸到了四大的PHD，进去后真能做出什么影响整个圈子的work吗？哎，每每想到这，心情就沉重了三分，如人饮水，冷暖自知，自己的水平是怎样的，只有自己最清楚，就像初高中随随便便就能考第一，大一大二翘一学年课都能拿A，是因为知道自己就是比起其他人强，但是真的到了PHD要搞research到时候，也是能清楚感觉到自己读的书太少！”书到用时方恨少“哪！高三可以几个月把高一高二三国杀+奥赛落下的吃完，但是真的面对人类边界的那些数学知识，我也实在只是一个普通人哪，尤其是最近读GCN相关的理论paper，那些证明只能让我感慨妙哉，让我来写我却只能摸摸脑壳。英雄联盟有个玩笑话:

不是你的分段，你不要碰

放到研究里，不也有

不是你脑子能搞懂的领域，你不要碰

我很自信我的水平是当得起香港中文大学博士的，但是，譬如让我成为一个MIT的博士，我只能呵呵了。这就是别人常说的，欲戴皇冠，必承其重吧。

但是我终究还是要努力去申请的。这也是这段时间想通的。关于随遇而安和尽吾志也的关系。我一直都是一个随遇而安的人，也因此对很多东西没什么追求动力。让我转变想法的是关于高中的一段话，大意就是高中是最美好的时光，因为它代表着无限的可能，代表着无限的选择。随着开始准备申请，我意识到，自己的学习能力是在逐渐下降的，而这种下降，也意味着自己未来选择的权利和机会是越来越少的。同时，作为一个master，而不是PhD student，我还有也是仅有申请PhD这最后一个机会，来提高自己的可能性。所以，在学习能力还在巅峰的最后几年，去努力成为自己想成为的人，才不至于让自己在没有这个学习能力，没有这个申请机会的时候叹息后悔。这才是“尽吾志也而不能至者，可以无悔矣”的真义哪，先有尽吾志也，才有无悔。哈哈，原谅我这个年轻人对于人生观的多变，不知道2030年的你看到这些会是怎样的想法，又会有怎样的人生观，这也算是我们生而为人很奇妙的一件事吧。

啊，其实还有很多sub-topic想说，但是已经三点了，我实在是得睡了，所以下次再说吧。最近总是中午才起床，拖拖拉拉就是两三点才开始办公，事情都拖着，每天还要两小时背单词，之后一定得最大化利用时间了！

Fighting!

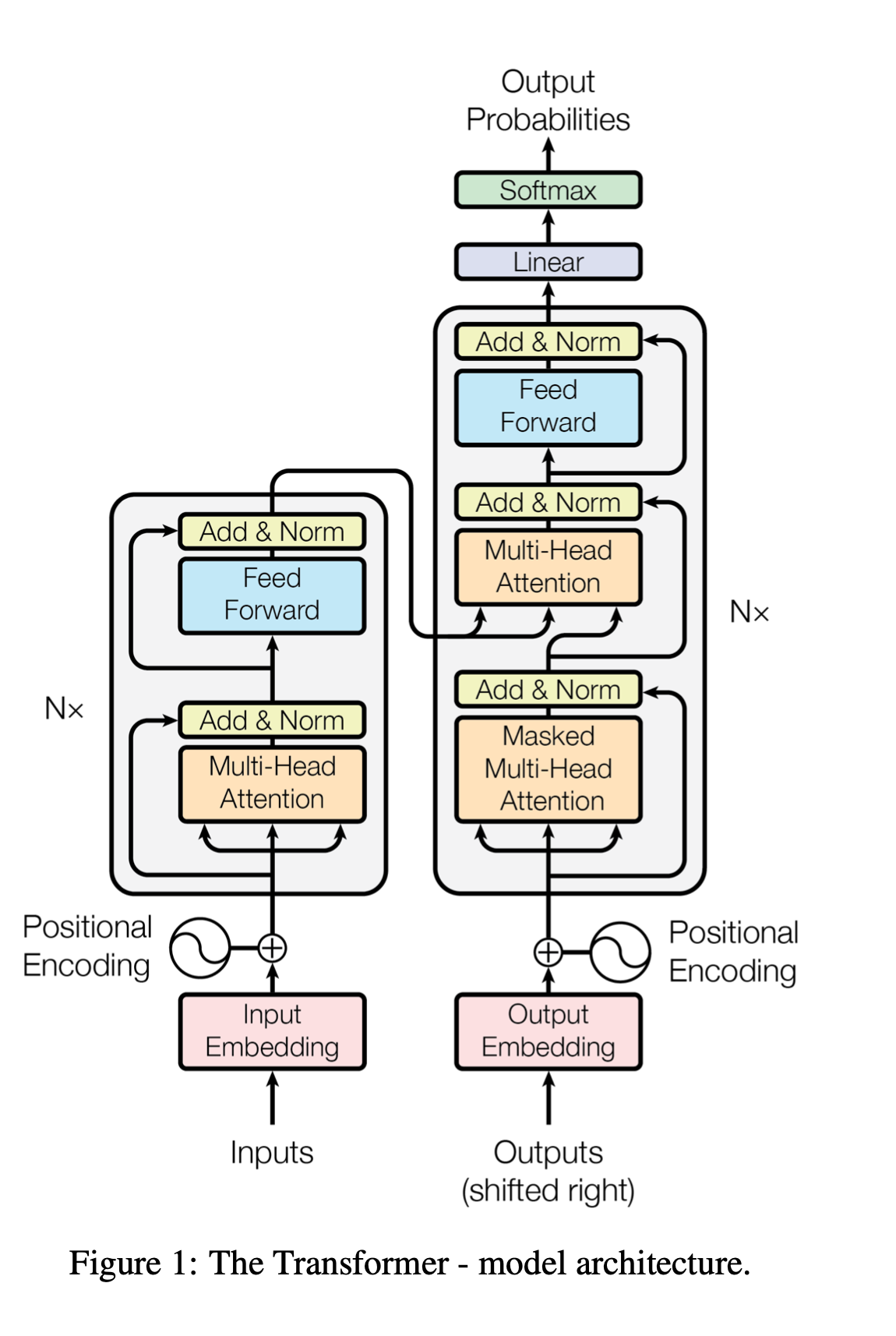
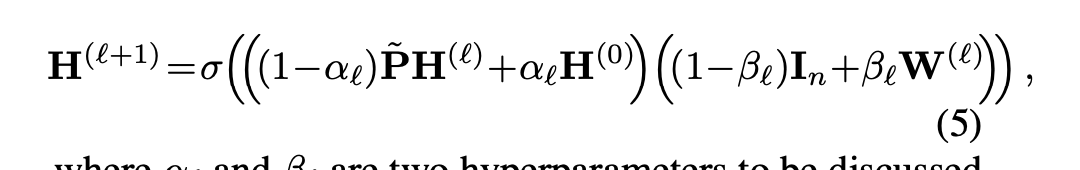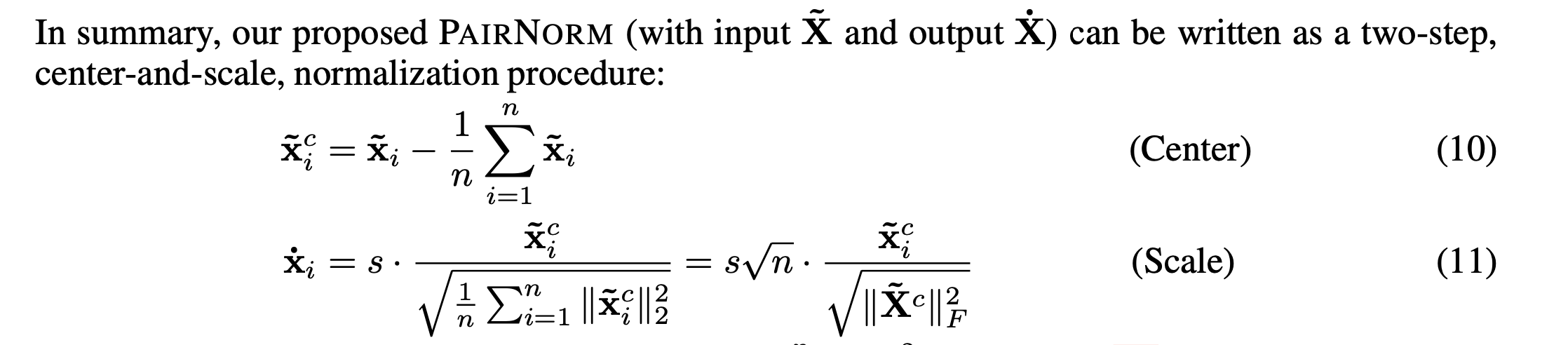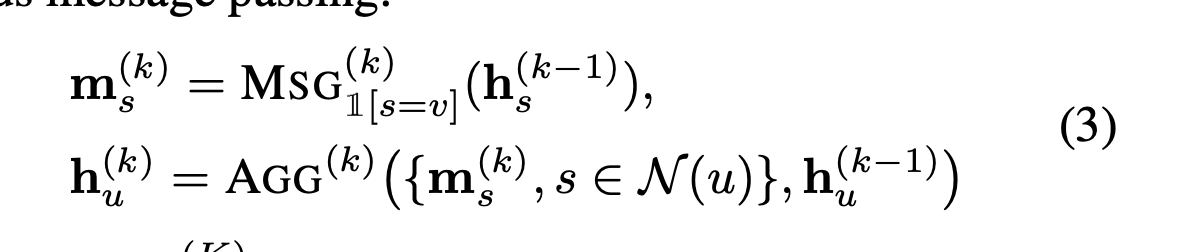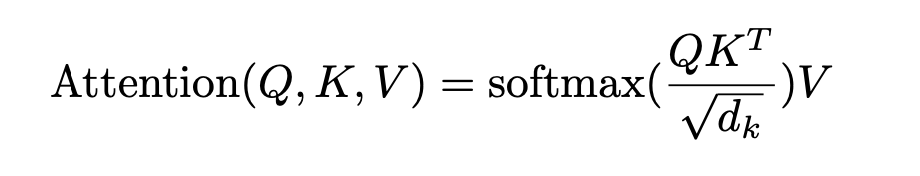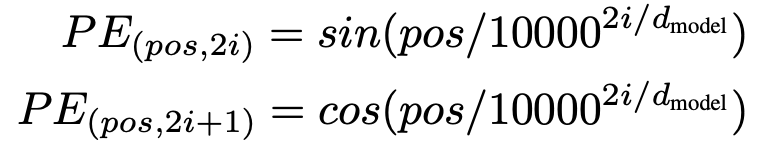前言。本文作于GCN横空出世（2017）的三年后（2020），想尽可能在简单易懂的情况下说清楚近年GNN的发展脉络。当然，凭我鸽子王的尿性，估计本来也就不会写的很翔实（简单是第一层，偷懒是第二层🐶）。

4th, March, 2021. Update: After a series of rejections by AI conferences, I note that I may look back on these papers and rethink why these papers can be accepted, i.e., review them in a positive and admired way instead of criticising them. Also, I try to pay attentions to the authors and institutes, and summarize the research style of different groups. This helps to understand the whole GNN community and “may” contribute to my PhD dicision.

最近GNN又看了一些ICLR2020的paper，加之之前积累的paper，对整个GNN的发展脉络有了比较清楚的理解，之所以想要记录在案，是因为发现：

• GNN有点类似CNN，是一个入门难度不高，效果又比较出色的技术。不像EDA里面各种子问题及现在的SOTA解决方案，要解释清楚就要半天。
• 现在的各种文章因为作者们的严谨及数学功底的雄厚，导致涉及内容过多，我要真正看明白的阈值太高（对不起实在是因为我太菜了），因此心里琢磨着要是能有一篇浅显易懂的综述，快捷的理清paper间的区别和发展脉络该多好。
• 现在许多GNN的paper其实真正technique部分的contribution很容易概括，当然所谓的research也不可能是一蹴而就 novelty、results什么的全都完爆previous work。只是很多paper的出发点都不一样，导致看起来paper间差异很大，其实在我看来现在GNN还是一个比较混沌的状态，等着哪位X kaiming大神来盘古开天。（或者说GCN这篇就算是开天了？）

Note：这篇文章完全是为我本人量身打造，是为了未来的我复习GNN的时候有个参考。因此我面向的读者是有了比较充足的CNN、Graph知识背景的。

开山老祖 GCN

这一段大部分是我的臆测。。可以直接看结论。

给一个irregular的grpah/point cloud，我们可以从频域(specture)和空间(spatial)角度去解决这个问题

• 频域角度就是图信号映射到频域后再做卷积操作。（直接copy from zhihu，原谅我这一块其实并不是很清楚，因为现在的大部分work都不会提specture这个东西了。。。而且本身这个对数学功底要求就有点高，也许我真的phd了可以花时间研究这个？单就目前纯水paper的角度，这个建议不要碰，1.上手难，2.现在大部分SOTA都是spatial）
• 空间角度大概就是直接从点/线的关系入手，用这些关系来表示某种message passing。messgae passing的意思很简单，就是说给一个点，它会把它自己的信息（feature）传输给它的邻点，同样，它的邻点也会把邻点的信息传给它。大概有点像社会学里面的信息传输，譬如李巍长得很帅，一传十十传百所有人都知道我长得很帅这样。。（我长得很帅这个信息就被所有人收到了，这样在他们那的信息就是：我有个朋友/朋友的朋友长的很帅）

这篇GCN做的就是，从频域角度出发给了GCN的公式：

$H^l$就是第l层的所有点的feature，$\bar{A}$是加上identity matrix的矩阵，D是degree matrix为了normalization（结果其实比较接近mean），W就是映射到另一个空间增加信息量。

然后发现这个公式其实可以从空间的角度很elegant的解释，GCN的每一层其实就是aggragation + combing（encoding）

• $\bar{A}H$ 其实就是对于任何一个点，将自己的feature，以及邻点的feature 累加起来，加个D就是为了normalization（$D^{-1}$ 其实就是mean），因为每次都累加层数多了这个值不爆炸了？而且有些点邻居本来就多怎么办？。
• $W^{l}$ 就是做一次combing啦，可以理解成投射到另一个空间增加复杂度（其实就是1*1conv，or FC，or MLP，哦，有的可能还会加个bias）

方法层面

GraphSAGE

这篇就直接不管specture了，直接从空间角度把GCN重新提了一遍，同时formally定义了aggregator这个概念，其实就是对于每个点，怎么将它自己及它邻点的信息聚合（aggregate）起来。然后还提出了几个方法。

• 不加自己的feature mean 。
• 加上自己的feature mean。。。
• LSTM。。。也许那个年代LSTM比较火吧。
• channel-wise的max sampling

注：aggregator其实总之不管是什么，都只要保证order-invarienty以及size-insensitivity就行了

GAT

这篇就是说attention效果这么好，我们也套用到GCN吧！（对不起这是我的小人之心🐶），实际上应该是：每个邻居可能重要性不一样，所以要加个attention！

a(i,j)就是点i对点j的重要性。但这个真把我秀到了，具体可以参见https://wadmes.github.io/2019/12/30/attention/

JKNet

这篇就是说DenseNet效果这么好，我们也套用到GCN吧！（其实background还是GCN层数过深，例如depth>2，就会出现oversmooth的情况，即所有离得近点的feature长的都挺像的。而离得远的点互相的connection又太小了，所以加个densenet就可以让他们connection不小了呀呀呀呀呀呀）

提到oversmoothing了就说下，其实直接原因是目前GCN的aggregation必须保证order invarienty，导致不像CNN里面的convolution kernel一样卷积时候可以带weight，想象一下CNN里面a pixel的右边是b pixel，传信息的时候用的是3*3kernel里面的(2,3)value，而b要传给a，就是(2,1)了，两个值不一样，所以不管传多少次都不会最后比较接近，除非(2,3) = (1,3)，这就是GCN现在的情况，因为GCN不可能还有方向这个概念，或者说，给一个点a，他有邻居b，c，目前还不可能能分出b，c。。

DeepGCN

这篇就是说ResNet效果这么好，我们也套用到GCN吧！

然后除了简单的加个residual connection，还提出了一个GCN上的dialated convolution，个人觉得是比residual 更重要/有效的一点。大概就是：regular CNN里面dialated convolution可以很轻松的跳一个选一个这样卷积，但是GCN不好操作因为每个点邻居个数都不一样，而且还是无序的。这里的做法就是对于每个当前点，给其他点按照feature的欧几里得距离来个排序，然后就可以跳一个选一个啦！（其实有点做point cloud里面dynamic graph CNN那味了）

Dropedge

这篇就是说Dropout效果这么好，我们也套用到GCN吧！

不过这里的dropout其实不同于CNN里面对feature的dropout（其实对feature的dropout在original GCN就用了），而是对weight的dropout，即每一层有概率的remove edge，（脑补一下，其实就相当于把GCN的weight全为1 改成了有些为0有些为1啊！）

Position-aware Graph Neural Networks

这个不是借用CNN的一些technique的理念，说下大概思路吧。

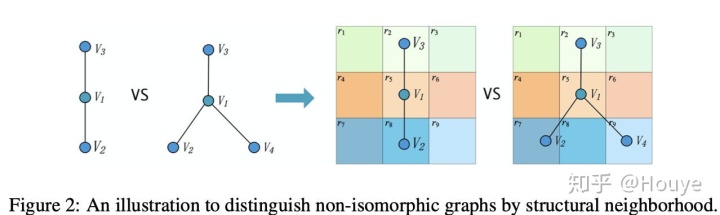
• 问题：GCN只能捕捉局部的structure 信息，比如：

  

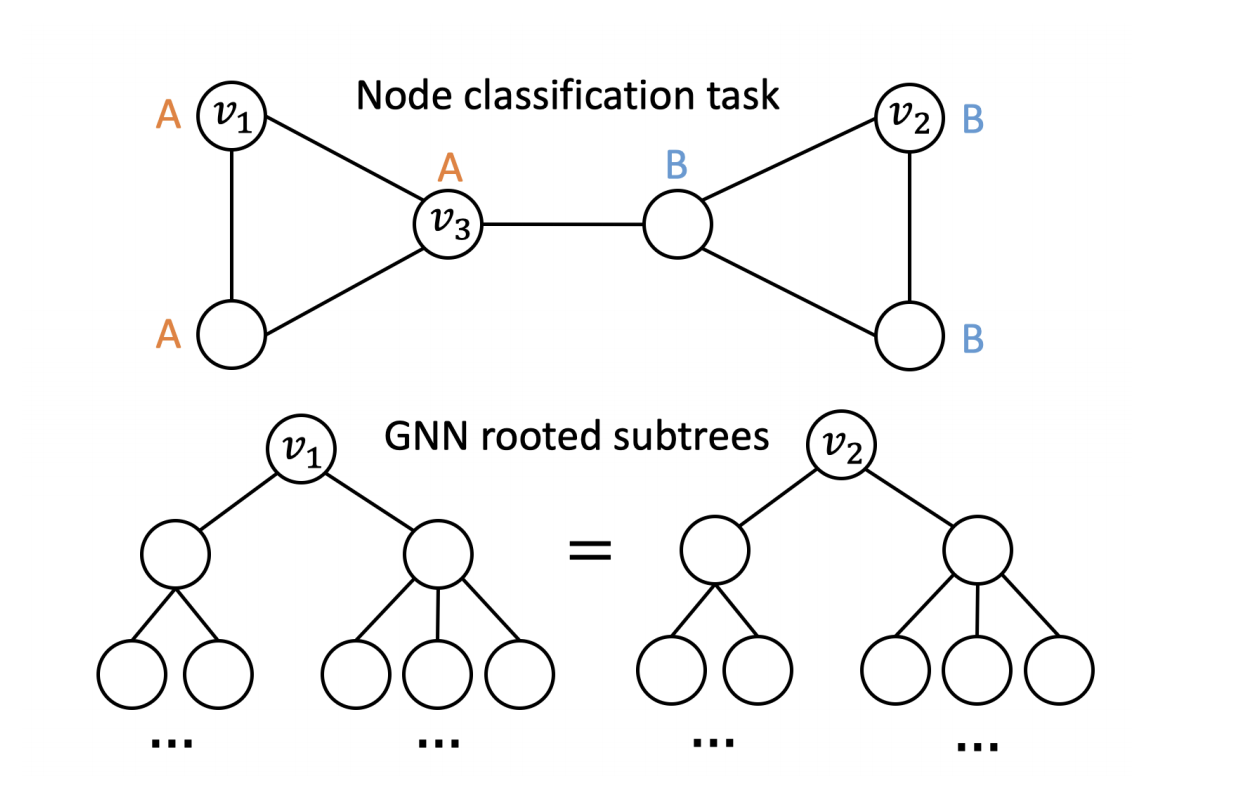
  不管怎样$v_1,v_2$（structurally isomorphic nodes）都是分配同样的label。那么怎么解决这个问题呢？

  node position can be captured by a low-distortion embedding by quantifying the distance between a given node and a set of anchor nodes

• 先说下workflow吧，

  • 给$clog^2n$个子集$S_{i,j}，i=1…\log n,j=1,…,c\log n$，每个子集会随机选择所有点，每个点被选中的概率为$1/2^i$,所以其实子集的大小其实是指数型增长的
  • PGNN的每一层operation如下，
    • 对于每个点，和每个子集里面的所有点（假设n个点）的featrue(假设d维) concat 起来->$n\times 2d$，如果子集里的点是距离为$k$外的（太远了），则return zero值（而不是concat feature）。接着把concat结果aggreate起来-> $2d$ （注意这里的aggregate也需要满足order invarianty！所以也只能用mean，max，sum等，作者直接用的mean）
    • 对于不同的子集的结果再用aggregate $c\log^2n \times 2d \rightarrow 2d$。

• 总结：这篇的theorem用了Bourgain Theorem去证明只要$c\log ^2 n$个就子集就可以preserve the distances in the original graph with low distortion。。。不过很多paper里面的theorem都是比较巧妙的，让人觉着遥不可及。但是这个work解决GCN只有local structrue的大概方法也是类似的：就是想方设法的介绍一些global information进去，这里是通过介绍子集的方法，相当于给子集中的每个点多了一个额外信息：属于哪个子集。打个比方，假设所有人只有性别这一个label，我和坤坤都只有三个男性朋友，一个女性朋友，这样一层GCN就无法通过信息传输判断我的label了，但是如果创造2个子集（身份），分别是 爱rap的同学 和 爱打篮球的同学，然后发现我有一个爱rap的同学，2个爱打篮球的同学，坤坤有3个爱rap的同学，这样我和坤坤的label就是不一样的了。

COLORING GRAPH NEURAL NETWORKS FOR NODE DISAMBIGUATION

引入了universal representations & separability的概念，claim MPNN不是一个universal representation。解决方法（甚至出发点）和上篇paper有点相似。大概就是给node attribute 相同的点 从k种颜色中随机选一个颜色标上，k为hyper parameter，这样就实现了universal approximation。有两个concern

• 若k不为 graph size （即所有点颜色都不一样），那么这种coloring sheme不是permutation invariance。这也是ICLR被拒的原因。
• k=1时，不就是所有点assign一个相同的颜色么。。没看懂。。。

GeomGCN

同样，这个也不是借用CNN，说下大概思路吧。

• 问题：1. 就像GIN说的（就这篇下面👇），现在基于聚合的都是垃圾，因为会将部分Non-isomorphic的图也给出同样的结果，如

  

  2. 同样的 有些graph里面可能有些子图其实是有相似结构的，那么为什么不利用起来呢？

• 基于以上两点，可以大概构思怎么解决 1. 将不同的node 当作不同的neighbor来聚合 2. 给每个node 加上一个能表示局部结构的node （这样局部结构相同的两点其实就可以share同样的feature了）

• 所以大概workflow如下：

  • 给每个点计算latent space上的node embedding，注意此处的node embedding是仅仅包含local struture 信息的（原文用了一些GCN之前的获取node embedding的方法，真的很纳闷为什么不直接用SOTA的GCN来获取node embedding）
  • 对于每个点centroid，它都有两种邻居：真实邻居，转化成latent space下的邻居（另一个时空下的恋爱🐶），然后将每个邻居按照与centroid在latent space中的位置关系分为不同的邻居（为了解决第一个问题）。这里的实验latent space是二维的，所以邻居只分了四种，左上右上左下右下。
  • 这样对于每种邻居，我们就分了四种点，这样就有四个aggregator，最后四个aggregator结果concat起来就行（因为总得保证是固定个结果嘛）

Generalization and Representational Limits of Graph Neural Networks

定义decide：一个GNN Q如果decide了一个图性质P，则说明图性质P不同的两个图，由Q产生出来的graph embedding也肯定不同。

这篇文章前半部分就是用一些例子证明了：

• （用一些反例）基于聚合的很多GNN不能decide很多很简单的性质。

Simple and Deep Graph Convolutional Networks

Use two simple techniques to make GNN deep

• Partially aggregate the input feature $H^0$, instead only aggregating previous layers features from its neighborhood

• Adding a partial skip connection part

• 

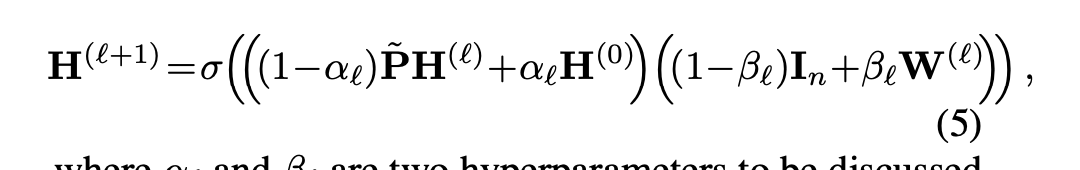
PAIRNORM: TACKLING OVERSMOOTHING IN GNNS

Another paper to handle with oversoothing issue in GNNs, i.e., cannot generalize to deep network.

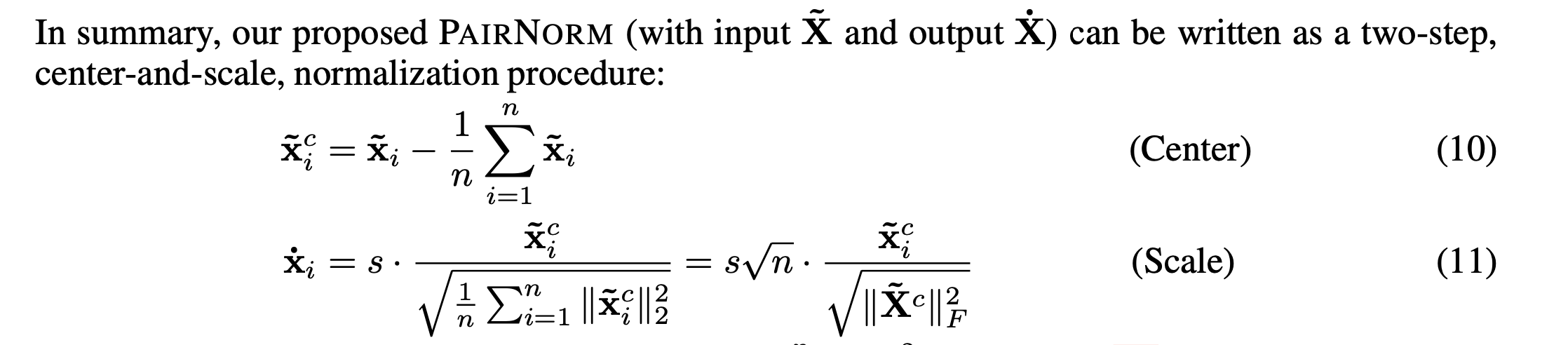
Here, n is the number of nodes.

The normalization is simply used for the output of each layer

Simplifying Graph Convolutional Networks

Non-linear 在很多任务中没什么用，GNN可以直接用一个很简单的linear model来表示：

$Y = softmax(S^KXW)$, where $S = normalized \ A$

理论层面

GIN

这个算是个人觉得最有意思的一篇了，大概就是说在座各位基于这种聚合的都是垃圾，最多也只能和从前的WL Test一样。https://wadmes.github.io/2019/09/14/GNN-GIN-GMN-study/

Weisfeiler and Leman Go Neural: Higher-order Graph Neural Networks

A very good paper that proves a similar conclusion with GIN. (the difference is that they use linear transformation instead of MLP, and finally claim that double the layers (which becomes MLP actually) can have the same performance with WL test)

And then propose a k-GNN based on k-dimensional WL test. Basically, the “supernodes” is all k tuples of the graph.

THE LOGICAL EXPRESSIVENESS OF GRAPH NEURAL NETWORKS

这篇（ICLR2020）大概就是接着上一篇GIN（ICLR2019）说，诶，确实以前的聚合（自己的+邻居的）都是垃圾，但我这个不一样了，对于每个点还有了个全局（readout）信息。

首先先从一个最简单的给点二分类的问题说起：如果要判断一个点是不是isolated node。我们是不是就没法正确分类了？因为true的点肯定没法传输信息。这个例子实在是妙啊。。

那么这个全局信息是什么呢？就是所有node feature的sum啦。。（ps。。头皮发麻）

WHAT GRAPH NEURAL NETWORKS CANNOT LEARN: DEPTH VS WIDTH

这篇文章的作者。。emm。。怎么说呢，一看就不是国人同时又是为计算机基础知识特别好的大神。

文章的证明需要比较强的计算机背景，不过结论很简洁易懂：

该研究证明，如果我们想让 GNN 为常见的图问题（如环检测、直径估计、顶点覆盖等）提供解决方案，则节点嵌入的维度（即网络宽度 w）与层数（即网络深度 d）的乘积应与图大小 n 成正比，即 dw = O(n)。

Approximation Ratios of Graph Neural Networks for Combinatorial Problems

这篇将GNN和distributed local algorithms 结合了起来，先证明了GNN和distributed local algorithms 是等价的，然后利用以前work对distributed local algorithms的研究得出的结论直接给出了GNN的一些结论。

大概就是现在两种GNN， MB-GNN 和 SB-GNN都比不上 VVC-GNN，定义分别是：

因此，提出了一个VVC-GNN。大概意思就是给别一个边的两个出口都assign一个port，使得所有点给它邻点的信息完全不一样。

最后实验就是用这个model + reinforcement learning 证明了 这个model可以解决很简单的组合优化问题，但是MB，SB都不可以。

在我看来，有个点是没解决的：

• 这种方法注定导致不能迁移到其他graph（相当于给每个edge的port一个人为的index）
• 这个方法训练时间需要很久，但同时不能用到其他graph。。也太扯了吧。

关于distributed local algorithms的定义，请参考 https://arxiv.org/pdf/1205.2051.pdf

Distance Encoding – Design Provably More Powerful Graph Neural Networks for Structural Representation Learning

添加了一个distance encoding to encode certain distance from S to a node u， 其中S是图中的一部分structure，想学的target structure feature就是S的feature，若S为全图，则为全图的feature(graph embedding).

这里的distance encoding 有比较复杂的formal形式，但是实验里面用的其实就是最简单的两点之间最短距离。

Design Space for Graph Neural Networks

Motivation:

• Surging new GNN tasks, with different requirements
• Large design space of GNNs

Design space:

• BN; Number of Pre-process layer (MLP); Number of Message Passing Layers; Sum/Mean/ and son on

Task space:

• Synthetic tasks: node features/ labels/ node/graph classification
• Real-world tasks: 6 node classification benchmarks from [26, 28], and 6 graph classification tasks from [14].

GraphGym

• Modularized GNN implementation
• Standardized GNN evaluation.
• Reproducible and scalable experiment management

Results:

• BN good!
• No Dropout good!
• PRELU good!
• SUM good!
• Adam good (compared to sgd)
• 400 epoch good than 100,200

However, besides these “common-sense” conclusions, desirable design choices for Aggregation, Message passing layers, layer connectivity and post-processing layers drastically vary across tasks

Tasks can be roughly clustered into two groups:

• (1) node classification over real-world graphs; with rich node features; GNN designs that can better propagate feature information are preferred;
• (2) node classification over synthetic graphs and all graph classification tasks; require graph structural information

How to determine the “best” design for a new task?

• using $M=12$ echor models to test the task,
• find the most similar task based on the rankings of the echor models.
• use the best design of the most similar task as the “best” design

Identity-aware Graph Neural Networks

Background

• MP GNN cannot distinguish nodes with the same computational graph.
• Although task-specific feature augmentation; is not generic and hamper the inductive power
• Previous works task specific; and not based on MP GNN->not efficient

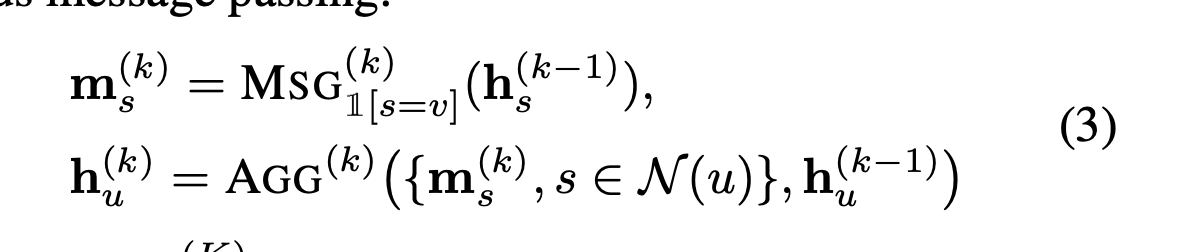
DropGNN: Random Dropouts Increase the Expressiveness of Graph Neural Networks

非常漂亮的文章！

大概就是GNN的upper bound是WL，那么有没有可能突破这个upper bound呢？方法是简单的randomly drop node，这样一个graph 就对应成了 一堆graph 的distribution，那么不同graph 的distribution大概率是不一样的！

这个问题是相同graph的distribution也可能不一样，除非randomly drop的次数足够多，就像投硬币一样。文章里面还给了solid proof about the probability of the distribution close to the real likelihood.

将statistics 里面的一些东西运用到graph里面来，感觉很有潜力啊！

Some other interesting papers

NEURAL SUBGRAPH MATCHING

Done by Stanford Group. The problem is to determine the presence of a given query graph in a large target graph.The key insight that makes NeuroMatch work is to define an embedding space where subgraph relations are preserved. That is, : If $G_v$ (k-hop neighborhood of node v) is a subgraph of $G_u$, then node v should be embedded to the lower-left of u. Such relationship is preserved in the embedding space by an elegantly-designed loss function:

Beyond Homophily in Graph Neural Networks: Current Limitations and Effective Designs

This paper discusses GNNs in graphs where connected nodes may have different class labels and dissimilar features.

Three techniques are used:

1. concatenate aggreated features insteaed of sum or mean them
2. Higher-order Neighborhoods, concatenate two-order neighborhood
3. concatenate (at the final layer) all learned ego-representations at previous layers

后记

写完后，忽然发现了一个也可以算巧合的规律吧？所有方法层面的work基本都是国人lead，但是理论层面的work却寥寥无几。这算不算是一种悲哀呢？方法层面的东西固然重要、效果好，容易发paper，但是理论层面的才是有可能真正推动时代进步的那个钥匙，不过似乎大家都对这种“不好发paper”、“没有确定性”、“难入门”的东西有一种共识性的排斥，算是一种悲哀吧！

其实自己何尝不是这样呢。做了五六个work，除了openmpl，其他的基本都是比较讨巧，迎着市场需求（学术圈热点）做的东西。这是这个时代的无奈，也是我个人的无奈吧，其实也是蛮想做一个沉下心学习研究一两年然后真正contribute to the development of CS的东西，可是现在还只是一个再过几个月要靠publication去砸PHD commitee脸的小小mphil；就算phd了也只是一个担心qualification、担心graduation的PHD student/candidate；就算当教授了也需要paper去争tenure啊；就算当了professor，也得对学生负责，在他没有成果前不可能让他做一些我自己都无法保证的东西吧？好像真正可以肆无忌惮做这种work的时间段只有achievement差不多时候的PHD year4/5了？

扯的有点多，说回GCN吧。总的看来，其实各种technique/theory还是在发展中的，不过里面确实还有很多可以发掘的东西，而且从功利化发paper的角度，不仅仅是Common GCN, 很多子分支，譬如point cloud，譬如heteogeneous graph（参考[https://wadmes.github.io/2019/12/17/heterogenous%20network/](https://wadmes.github.io/2019/12/17/heterogenous network/)） 这些子分支都是水paper的好方向哪。。

另外就是虽然所有paper的conclusion或者method看起来很简单：这不是本科生都能想到的吗？但是里面的story writing绝对是我得好好研究的：怎么将一个简单的solution包装的很elegant，它解决什么问题的？有什么理论去支撑的？实验怎么设置？这里面都是学问啦。总之，虽然novelty不够，但是发现了这些work的一些共同点：

• 大部分都有看起来牛逼哄哄的theorem/proof（对不起因为大部分theorem我没有仔细看，所以只能暂时说看起来。。。）
• results部分不会特别出彩，但肯定不是完全比不上别人。1% improvement 🐶，当然如果是专为解决特定问题的，譬如logical问题的那位，就是可以完爆了。

When we finish a paper draft by latex, we may find it difficult to directly use Grammarly to check the grammar since our paper is a .pdf format.

Here is a simple instruction to use Grammarly for your paper. If you have some other more elegant methods, feel free to leave a comment here. :)

Here are the steps:

• Copy the text in the paper and paste it into VSCode

• Replace all “\n” terms into space “ “ terms

• Copy the processed text in VSCode and paste it into Grammarly

• Find the error and fix it.

  

离ICCAD还有三星期的时候和老板说想放弃投ICCAD，最后在他的“威逼利诱”下，再加之自己的年轻气盛还是答应了并全力以赴的完成了。想想也是蛮了不起的，不过最后一两个星期实在是太累了点，希望以后还是少点这么肝的时候吧。

这大概一个月，一边做proj一边就有新的感触，每有一个感触，都会自己先记一笔，然后不知不觉的备忘录上就塞满了感触。。。现在一次性都记下来当作以后的吸取教训吧。

Idea & Paper Review

前面两个proj 都分成了c++ 和python/pytorch两个板块，因为比较尊重本科生的意见，所以都让他们先选负责的板块（所以都是选的python）。但是有个严重问题：pytorch部分往往和整个proj的idea相关，所以让本科生看paper 找idea实在是好刚没用在刀刃上。因此 两个proj都耽误了比较长的时间。好在自己看paper 总结idea的水平还是比较高了，后面都很快的调整好了方向。

以后在我看来本科生的帮助应该是：

• 跑实验这种大家都需要时间成本，而且学习成本较低的work
• 画图，implementation就取决于本科生的学习能力和是否有过类似经验了。倘若我和ta都没学过，那让ta来学一下画图也可以（学习成本一个人花费就可以了）
• 整个idea方向，除非是比较厉害的本科生（这么看我当年其实还是蛮厉害的，在南科大work都是我来看paper想idea），否则应该是我来看paper 总结，想idea，同时简单的传达意思给ta。毕竟确实我看paper的经验，水平肯定高过大部分本科生的。

最后再吐槽下吧，好羡慕南科大有那么多本科生帮忙，然后本科生也有各种1/2/3作paper，实在是双赢。CU的本科教育就花在了倾庄、人文教育上了（当然有research，但是比起内地学校有组织的research还是差远了）。

Coding style

这是看了DGCNN的mit学长的code发出的感慨。感觉任何语言，尤其python，必须要有一套自己习惯的coding style，包括但不限于：

• argments
• i/o
• error exception handling
• model architecture

这样的话，自己implementation的时候会方便很多，同时本科小朋友帮忙跑实验也会简单很多（改参数就可以）。哦对了，还有一个要习惯用git。。

Torch Tensor Operation

这算是implementation时候的一个点吧。之前习惯了for loop，这次用多了pytorch tensor后发现实在是太爽了。不仅是速度提升（1000x），整个code 也elegant很多。说下从for loop 转成tensor operation的大概idea吧：

• 如果index 不影响operation的话，可以直接用tensor[:]操作
• 如果影响就需要 生成一个index tensor
  • 灵活利用torch gather（有一串index 和一个index对应的value， 想通过index取出所有对应value）
  • 利用torch where 来代替 if else

晒一下自己生成kbbox（对于每个点，return k个最近的且两点bbox间没有第三个点的所有neighbors）的elegant code吧（对比for loop):

For loop version:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41

for size in range(SIZE_OF_NET):
    num_of_sample = int(size)
    data = train_data[size].cpu()
    # data = train_data[size]
    if(len(data) == 0):
        continue
    index = torch.zeros([data.size(0),data.size(1),num_of_sample]) #B,N,K
    for N in range(data.size(1)):
        #initialize all value as current node index N
        index[:,N,:] = N
    #for each batch B
    max_sample = 0
    print("PROCESS ",size)
    for B in range(len(data)): 
        #for each node N
        if(B % 1000 == 0):
            print("PROCESS ",size,B)
        for N in range(data.size(1)):
            sample = 0
            #We then check each point Q: whether the bounding box between Q and K has no other points, if yes, we add Q in index[B,N,:]
            for Q in range(data.size(1)):
                if(Q == N):
                    continue
                #Coordinate of Q related to N
                C_QN = data[B,Q,:] - data[B,N,:]
                is_index = True
                for J in range(data.size(1)):
                    if(J == Q or J == N):
                        continue
                    C_JN = data[B,J,:] - data[B,N,:]
                    if ((C_JN*C_QN) > (C_JN * C_JN)).min():
                        # print("Q cannot be index of N due to J",C_QN,C_JN)
                        is_index = False
                        break
                if(is_index):
                    sample += 1
                    index[B,N,sample] = Q
            if(sample > max_sample):
                max_sample = sample
    print("PROCESS ",size, "max_sample: ",max_sample)
    torch.save(index[:,:,:max_sample+1],"../../data/tree/"+str(size))

Tensor operation version:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43

#data : raw distance data (B,N,2)
data = tensor
if(len(data) == 0):
    continue
# print(tensor.size())
B,N,_ = data.size()
# data = train_data[size]
# print(tensor[0])
#inner : (B,N,2) * (B,2,N) = (B,N,N )
inner = -2 * torch.matmul(data,data.transpose(2, 1))
xx = torch.sum(data ** 2, dim=2, keepdim=True)
#pairwise_distance: relative distance between N1 & N2 (B,N1,N2) 
pairwise_distance = -xx - inner - xx.transpose(2, 1)
# print("pairwise_distance",pairwise_distance[0])

# BNN2 = data.view(B,N,1,2).repeat(1,1,N,1)
# BQQ2 = data.view(B,1,N,2).repeat(1,N,1,1)
# print("BNN2",BNN2[0][0])
# print("BQQ2",BQQ2[0][0])
#BNQ2: value in (b,n,q) is the relative coordinates between node n and node q at b_th batch.
# BNQ2 = BNN2 - BQQ2
BNQ2 = data.view(B,N,1,2) - data.view(B,1,N,2)
# print("BNQ2",BNQ2[0][0])
#CQN: value in (b,n,q,j) is the relative coordinates between node n and node q at b_th batch.
#CJN: value in (b,n,q,j) is the relative coordinates between node n and node j at b_th batch.
#UPDATE: The view step here is not neccesary since pytorch will automatically scale the tensor shape
CQN = BNQ2.view(B,N,N,1,2)
CJN = BNQ2.view(B,N,1,N,2)
# print("CQN",CQN[0][0])
# print("CJN",CJN[0][0])
#BNQJ: value in (b,n,q,j) indicates that when n is the centroid, whether j is in the bounding box of q and n (and such makes q not connected to j)
#True means the j influences q
BNQJ = (CQN*CJN > CJN*CJN).min(-1)[0]
# print("BNQJ",BNQJ[0][0])
#BNQJ: value in (b,n,q) indicates that when n is the centroid, whether q cannot connect to n
#True mans q cannot conncet n
BNQ = BNQJ.max(-1)[0]
# print("BNQ",BNQ[0])
#For those q who cannot connect to n (which is exactly True in BNQ), we assign a large distance value(10000)
_,index = ((pairwise_distance - (BNQ.long() * 10000))).topk(k=4,dim = 2)
# print("index",index[0])
# exit()
torch.save(index,"../../data/tree/kbbox_"+str(i)+'_'+str(j))

总结

这个work应该是自己这么多work里面最满意的一个了？虽然比较仓促，但是整个story是连贯的，对应方法也不是和一般dl-based work一样讲究一个玄学，基本都是有规律有原因能解释的。最后的结果也是比较满意（最后两三天的时候加上了FLUTE的结果实在是不太行，临时把FLUTE remove了，最后一天才算出结果。。也是没谁了）

这个要是结果ICCAD没中可就滑稽了。投paper这个东西就真的可以叫做玄学了。ß

建议配合 https://www.bilibili.com/video/av56239558?from=search&seid=14406218127146760248 食用。

关于read paper：我个人觉得有两块要读（思考）：一块是算法上，有什么interesting或者amazing的算法值得学习。另一块就是经验、思想上，作者是如何提出这个方法的，这个方法背后蕴藏了什么思想/经验。

Background

• RNN不利于parallelization
• Attention可以无视sequence距离挖掘信息。（我爱这个笑着眼睛像月牙弯弯每天都像阳光一样点亮我的你-> key information：我爱你）
• 如今的attention（16年）仍然是和RNN一起出现(used in conjunction with recurrent network)
• 现在的work：要么不能并行。要么可以并行（例如CNN）却不能挖掘远处关联。（我爱月牙弯弯）
• Tranformer：第一个完全利用self-attention计算input和output的representation。（不用RNN，CNN）

Include 反义词： preclude 排除，杜绝：This inherently sequential nature precludes parallelization within training examples

albeit：尽管

Model Architecture

Overview:

1
2
3
4

At each step: (sequence to sequence should be generated step by step)
	middle sequence z = Encoder(Input sequence x(我爱你))
	output sequence y_t = Decoder(z,y_{t-1})
	注意：图中右下角的output为之前的输出。

Encoder

• LayerNorm(x + multi-head(x))
• LayerNorm(x + feedforward(x))
• keys,values,querys: input x

Decoder

• Addtional sublayer compared with Encoder: Masked attention layer(ensures that the predictions for position i can depend only on the known outputs at positions less than i.)

• Keys, values: middle sequence from encoder

• querys: Masked multi-head attention

Self-attention

A mapping from a query and a set of key-value pairs to an output

output: a weighted sum of the values, where the weight assigned to each value is computed by a compatibility function（适合性方程？总之就是计算相似度） of the query with the corresponding key.

$Q: [seq,d_k], K:[seq,d_k],V:[seq,d_v]$

$seq$: sequence length

注意 原x dimension 为$d_{model}$， 经过linear projection转化为 $d_k,d_v$ dimension

Multi-head

$x:[d_{model}] => [h *d_v]=>[d_{model}] $

h：head数目。（multihead最后concat起来，所以是$h*d_v$）

再经过一次linear transform到$d_{model}$

Positional Encoding

常见的position方法就是one-hot encoding，但显然不能input dimension匹配，而且若用one-hot encoding 直接sum 未免显得太蠢。

Transformer提出了利用正余弦的方法：

PE即为目标embedding。pos为word所处位置，2i即为 $d_{model}$中的维度之一。

• PE(:,x)即为$x_{th}$ dimensition下所有position的维度。 可以看到是一个周期函数
• PE(x,:)即为$x_{th}$ position下的embedding，是一个从波长为2pi 到 10000 * 2pi的函数。

但这里反直觉的是 PE是和input直接相加。而不是concat。。。 奇怪呢。

Dropout -> Residual -> Layer Normalization (Some papers claim that layer normalization should be in the sub-layer instead of behind residual summation)

Why self-attention

• # of operations
• Parallel
• path length between long-range dependencies in the network

Results

• Dropout 效果明显

我是个很少看剧的人。在我看来，冗长的剧情、尤其是毫无营养又冗长的剧情、尤其是毫无营养又冗长的宫廷剧实在是浪费生命。不过我为数不多的几次看剧都是真香结尾：大学的射雕英雄传，信号真香了，这次的1988也真香了。用真香这个字眼其实也不太准确：我还是对豆瓣高评分的事物抱有期待的，毕竟自己也只是个喜好和大众口味很匹配的芸芸众生之一。

照例。写一些自己印象深刻的点。

乌邦托

胡同里的所有人都太温暖了，温暖到我觉得这只可能是个乌邦托。德善很想被疼爱，但是只有两个荷包蛋时还是说自己不用，虽然自己其实也很委屈。爸爸知道了德善的委屈后，也可以如朋友般的和德善坐着聊天：”德善啊，对不起，爸爸也是第一次做爸爸。。“。善宇怕妈妈担心，把妈妈做的盒饭在进门前全吃完了。阿泽在知道爸爸的想法后，坦率的支持爸爸：“我只希望爸爸能过得幸福，毕竟爸爸也有自己的人生。”。正焕知道妈妈的情绪后，故意搞砸家里的事情。。。

虽然只是乌邦托，但是发现，做一个温暖的人、细心的人是真的很好哪。这些品质可以不被外界事物影响，留在自己身上一辈子，并且可以温暖到周边的人，这不是很幸福的事吗？其实说起来，从小寄人篱下的我从前倒挺会察言观色的，说好听点就是细心体贴，不过初三过后性格实在是变得太多太大条了，开朗如娃娃鱼可以，但是娃娃鱼好歹还是个人生导师、情商拉满呢，哪像我技术也不行，情商也不够，细心也丢了。

喜欢

不知道是逛虎扑知乎微博逛多了，还是自己变得现实了。

看完剧，想想自己。好像丧失了十几岁的那种喜欢，那种只想无条件对喜欢人好的喜欢，现在的自己变得很担心自己陷进爱情里，担心自己对她太好就是“舔狗”。其实想想，无条件对喜欢的人好就会是丧失自我的舔狗吗？恰恰相反，因为这些想法而丢了纯真的喜欢才是真的丧失自我，不是女方的舔狗，是“世俗”的舔狗。

什么是少年感？少年感是阿泽跟着去卫生间，还假装抽烟照顾德善的情绪。是正焕看着电影义无反顾的开车回去。是善宇的喜欢就是喜欢。很多时候，我们做出的选择是基于利益判断的，能赚钱是正收益，能提高ta对我的好感是正收益，如果付出的抵不上回报带来的数学期望，我们就不做了。但若尚为少年，怎么会考虑这么多东西？意气风发的少年是纯粹简单的。我喜欢你就是喜欢你，就是和你在一起就会很高兴，你不在就感觉要死了。所以会对你好，会吃醋，会关心你的动态，会照顾你的情绪。这些都是因为我喜欢你，也只是因为我喜欢你，如若有其他的原因，譬如希望在一起，那也变味了。

另外，还有一个也许看了这部剧的所有人都会同意的想法：爱就要大胆表现出来，命运不仅仅是偶然，是许多次要做出选择的瞬间组成的，让人讨厌的不是红绿灯，也不是时机，而是我的无数次犹豫不决。其实不仅仅是爱情，还有亲情，友情，许多东西都是如此，我爱你，所以我会表现出来，表现在方方面面，就像春天到来，你能闻到花香、听到鸟鸣，感受到舒服的阳光一样。

阿泽

比起简直就是初中前我的翻版的善宇，阿泽就是我的白月光啊！那种特别喜欢的人，那种特别想成为的人。温润如玉波澜不惊的性格真是太对我胃口了（我也不知道我现在怎么就是娃娃鱼的性格）。再想想自己高三努力的样子，发现我这个人真是个一辈子下来可以变化很大的角色。

像之前提到的，他很温暖，会照顾他人的情绪，娃娃鱼生气只有自己不知道善宇谈恋爱的事时立刻跳出来说自己也不知道（虽然撒谎很拙劣）。他对于自己的喜欢很坦率简单，我喜欢德善，喜欢女人的那种喜欢。他也很真实，放弃了自己喜欢的女孩后，会流泪难过，知道对方的心意后，又很直接的吻了上去，而不是像成年人一般有这样那样现实上的顾虑：那样多累啊？他还有我最想有的一点品质：知世故而不世故。采访了很长后，没有生气，而是说很晚了，让社长和他们一起吃晚饭。

就像弹幕说正峰的一样，阿泽也是“吾辈楷模”啊。希望自己以后，也可以成为一个如他般温柔细腻、知世故而不世故，一眼看过去就是干净简单的人。

自己的回忆

好像每个人都能从这部剧里面找到代入感一样，很多男生是正焕，是啊，青春期的男生，有几个会如阿泽善宇般直率的表白自己的心意呢。而我，肯定就是善宇了。所以从一开始就对这个男生有着先天的好感，懂事的令人心疼、会小心翼翼的照顾妈妈的想法，成绩也挺好，看着他穿白大褂的样子真有点恍惚：就好像我是医生一般。

同样也有一个院子长大的玩伴，不过自己不会表达想法的缺陷也让整个回忆没有剧里那么多友情有关的故事。有次，我和老辉看到肖华正在哭着拦着正扭打在一起的父母，我们两个只是苦笑：没有后续的行动了。我们两个也都有过类似的经历，所以苦笑，我们两个都不是那么温暖照亮他人的人，所以没有后续了。我想，如果是剧里面的任何一个少年，都会去安慰他吧。

剧看完了，其实更多的还是恍惚、难过、不舍。不仅仅是对剧，还有对剧里所代表的那段时光和感情。我已经不是中学生，甚至大学生都算不上了，学生时代的爱情和我估计也是没什么缘分了，和家人邻里也不可能有长时间的相处了，朋友好像也只有博一一个可以称为挚友。

不过也不算太糟：学生的爱情不可能了，但我还可以如少年般的去喜欢一个人。家人邻里不能长时间相处，但我也还可以做一个温暖的人，朋友有博一还不香吗，博一这样简单的人世上能碰到便算作有幸了呢！

差不多也到结尾了，写完这一通，好像也活得明白通透了一点，希望自己如自己所愿，做一个简单的少年。

三月过去了一半，整个二月，包括这已经过去的三月，都是颓颓的在宿舍度过的。这段时间每天做些什么呢？

十点多迷迷糊糊起床，玩手机到十二点，然后煮饭吃饭到了下午两点，稍微刷下虎扑知乎加写下代码，哦豁又要吃晚饭了。晚饭一过，就是各种娱乐活动了，913吃鸡，之前的剧本杀，现在的冬日计划，还有打了好几遍的三国志。。。

发现脑子这个东西还是得经常用经常转。之前划水的时候以到下午头晕的不行，但是有天强逼着自己学习写code，居然就不晕了。呵呵，我这叫做富贵病吗？

感觉不能这么浪费自己生命了，至少白天不能再手机综合征下去了。（其实颓的很大一个原因，是真的眼前这个OpenMPL的coding太过烦人，不过索性最终还是在今晚解决了，希望以后可以更有朝气的做接下来的许多许多事情。）

工作方面就是这样，说起来随着疫情的严重，intern的日期可能也需要变化，可能要推迟到下学期？不知道，但总之得尽快和老板确定。什么时候确定？等我openmpl搞定后才有底气说吧：毕竟确实划了太久水。

发现自己现在是个看得很开的人，不管是感情还是事业。有点命中有时终须有,命里无时莫强求的想法在三观里了，很多东西不太愿意投入太多的热情和希望，可能是害怕失败后的失望？不论好坏，但至少大部分事物不会让我捶胸顿足，喟然叹息，感觉也是成熟的一个小小标志吧。

最近唯一让我有点情绪的是妹妹的事。和妹妹视频，五岁的小孩子一句话不说，然后眼泪就流了出来。这么小就有了难以承受的心事，这么小就得寄人篱下 没有父母的照顾，这么小就眼泪憋不住的无声的流。看着真的揪心难受，既然选择了做父母，为什么就只管生不管养呢。不希望她重蹈我的覆辙，她这么可爱 ，这么漂亮，她值得拥有自己人生的幸福。

不过家家有本难念的经。我为我妹妹的人生叹息，我爸的人生也活得挺糟糕：生意上的不顺、女儿的身疾，都让这个中年人压着担子。哎，他的担子何尝不是我的担子呢。

今天忽然看到詹青云是12届的CU本科生，忽然惊了一下，想到自己14年入学的时候唯一报名的国辩队，没准当时她也在台上。然后觉得自己的青春这一点上挺可惜的，唯一报名的原因是确实当时只对这个有浓厚的兴趣，但是碍于懒惰，碍于一般家庭出生的短视，碍于自己的懦弱，最终还是没有去参加复试。也许参加了会有很多全新的体验、很多新的朋友、自己的思想也能系统化、逻辑化，对自己人生规划也会健全很多。

不过往者不可谏，来者犹可追。未来可能还会有这种辩论的机会（哈哈，不过就算有机会，也没有时间去准备、去充实自己了吧？），再不济，其他喜欢的东西一定要去追求一下。Follow your heart。

药效好像快到了，得睡了，晚安。Neway。前几天那个超大月亮确实很大，希望未来的某天你再看到月亮的时候，你找到了那个爱你的人。

optimized (multi-stitch version) dancing link

Here, I list the pseudocode of this algorithm, I didn’t implement it since it wasn’t critical for my journal…

But If you are required to implement a DL with dynamic working stitches. Hope this piece of code helps you. :)

The basic requirement of “dynamic” is:

• Given a working stitch k in each polygon, the alg construct corresponding coloring rows in the dancing links.

  Note that we need exactly k working stitches instead of # <= k (Since the optimality of DL is constraint by the row order, for example, if one polygon $p$ contains three stitches, then the rows indicating $p$ at beginning should be the coloring solution without working stitch, following is the # of exactly one stitch… and so on

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

def insert_exactly_k_stitches(k):
    for p in parent_node:
        if (|stitches_p| >= k):
            recursive_insert(k,stitches_p,selected_stitches)

def recursive_insert(k,stitches_p,selected_stitches):
	if(k>0):
        for(stitch in stitches_p):
            if(stitch not in selected_stitches): #select the stitch edge which has not been selected (to ensure exactly k different stitches are selected(working))
                stitch = selected_stitches[k-1]  
            	recursive_insert(k-1,stitches_p,selected_stitches)
    else: #k = 0
        #For the layout, one working stitch increase exactly one subcomponnet, therefore, there are pow(3,k+1) rows if we didn't consider the same coloring constarint(such as 1-1-1 for 3 sub-components).
        # For example, given two working stitches, which divide the polygon into three subcomponents, the total possible coloring solution for TPLD should be:
        #0-1-0,0-1-2,0-2-0,0-2-1,1-0-1,1-0-2,1-2-0,1-2-0,2-0-1,2-0-2,2-1-0,2-1-2
        divide the polygon into |selected_stitches| features
        recursive_color(|selected_stitches|, coloring_results)
 
def recursive_color(h,coloring_results):
    if(h>0):
        for(color in possible_colors):
            coloring_results[h-1] = color
            recursive_color(h-1,coloring_results)
    else:
        if the coloring is illegal constraint by selected stitches:
            continue
        #NOTE: here we may not need to remove illegal coloring! Guess why? because it doesn't influence the optimality, only possible efficiency is influenced. Since we certainly call insert_exactly_k_stitches(0), insert_exactly_k_stitches(1), insert_exactly_k_stitches(2)... and so on. If we delete this part, it means that the alg not onlt inserts exactly k stitches, but also working stitches whose number less than k
       	else:
            insert row according to the coloring results

for 循环中新建structure

如果直接用 Structure a = Structure(args)， 这个loop里面的a都是一个address

解决方法：new

1

liwei* a = new liwei(i);