Multiple stitch DL implementation的那些事

optimized (multi-stitch version) dancing link

Here, I list the pseudocode of this algorithm, I didn’t implement it since it wasn’t critical for my journal…

But If you are required to implement a DL with dynamic working stitches. Hope this piece of code helps you. :)

The basic requirement of “dynamic” is:

• Given a working stitch k in each polygon, the alg construct corresponding coloring rows in the dancing links.

  Note that we need exactly k working stitches instead of # <= k (Since the optimality of DL is constraint by the row order, for example, if one polygon $p$ contains three stitches, then the rows indicating $p$ at beginning should be the coloring solution without working stitch, following is the # of exactly one stitch… and so on

def insert_exactly_k_stitches(k):
    for p in parent_node:
        if (|stitches_p| >= k):
            recursive_insert(k,stitches_p,selected_stitches)

def recursive_insert(k,stitches_p,selected_stitches):
	if(k>0):
        for(stitch in stitches_p):
            if(stitch not in selected_stitches): #select the stitch edge which has not been selected (to ensure exactly k different stitches are selected(working))
                stitch = selected_stitches[k-1]  
            	recursive_insert(k-1,stitches_p,selected_stitches)
    else: #k = 0
        #For the layout, one working stitch increase exactly one subcomponnet, therefore, there are pow(3,k+1) rows if we didn't consider the same coloring constarint(such as 1-1-1 for 3 sub-components).
        # For example, given two working stitches, which divide the polygon into three subcomponents, the total possible coloring solution for TPLD should be:
        #0-1-0,0-1-2,0-2-0,0-2-1,1-0-1,1-0-2,1-2-0,1-2-0,2-0-1,2-0-2,2-1-0,2-1-2
        divide the polygon into |selected_stitches| features
        recursive_color(|selected_stitches|, coloring_results)
 
def recursive_color(h,coloring_results):
    if(h>0):
        for(color in possible_colors):
            coloring_results[h-1] = color
            recursive_color(h-1,coloring_results)
    else:
        if the coloring is illegal constraint by selected stitches:
            continue
        #NOTE: here we may not need to remove illegal coloring! Guess why? because it doesn't influence the optimality, only possible efficiency is influenced. Since we certainly call insert_exactly_k_stitches(0), insert_exactly_k_stitches(1), insert_exactly_k_stitches(2)... and so on. If we delete this part, it means that the alg not onlt inserts exactly k stitches, but also working stitches whose number less than k
       	else:
            insert row according to the coloring results

for 循环中新建structure

如果直接用 Structure a = Structure(args)， 这个loop里面的a都是一个address

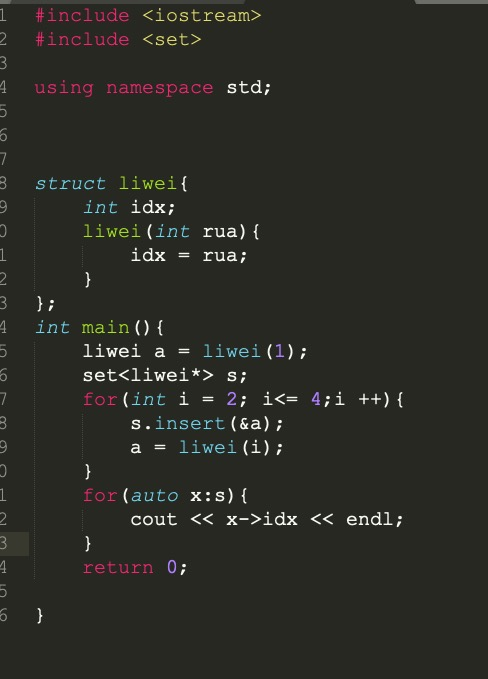
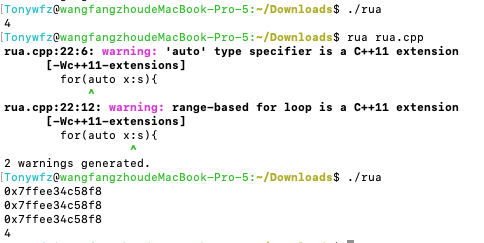
解决方法：new

liwei* a = new liwei(i);