Introduction
problem
difficult to simultaneously buffer the input feature maps, the output feature maps, and the filter weights in limited internal accelerator memory.
Previous method
use large SRAM buffers (up to a few MBytes may be used). drawback: large amounts of memory are not affordable.
Another point/direction:
data reuse , is determined by the dataflow schedule of computatio
Previous work: the working set of these innermost loops fits the available internal storage
drawback: existing models have not been adapted to explicitly application managed buffers, which constitute by far the most common memory architecture template for CNN accelerators, therefore, overestimate internal storage requirements
Contribution of this work:
- new analytical memory performance model to evaluate dataflow schedules
- best dataflow schedules
- applied it on the case study of the design of a flexible CNN accelerator for deeply embedded Systems-on-Chip.
Background
Convolution loop-nest
1 | // M output fmaps loop |
Goal
The problem consists in minimizing the number of memory accesses to the off-accelerator memory given a limited local buffer capacity.
Reuse in convolution
- Input feature maps
- Output feature maps
- Weight
the reuse of a reference is carried by a loop if the same memory location is used by different iterations of that loop
However, unless the entire working set fits the local buffer, this reuse cannot be taken full advantage of.
Reuse buffer
Data cache
Application-managed scratchpad memories
partitioning the local reuse buffer in a set of application-managed buffers,
Data Locality Optimization
reordring
titling
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23// output fmaps -- loop on tiles
LTOF: for (mm = 0; mm < M; mm += mss)
// input fmaps -- loop on tiles
LTIF: for (cc = 0; cc < C; cc += css)
// spatial -- loops on tiles
LTSY: for (yy = 0; yy < E; yy += iss)
LTSX: for (xx = 0; xx < E; xx += jss)
// output fmaps -- tile loop
LOF: for (m=mm; m<min(mm+mss,M); m++)
// input fmaps -- tile loop
LIF: for (c=cc; c<min(cc+css,C); c++)
// spatial -- tile loops
LSY: for (y=yy; y<min(yy+iss,E); y++)
LSX: for (x=xx; x<min(xx+jss,E); x++)
// kernel -- tile loops
LFY: for (k=0; k<R; k++)
LFX: for (l=0; l<R; l++)
{
p = I[c][y*S+k][x*S+l];
w = W[m][c][k][l];
O[m][y][x] += p*w;
}
Method
Analytical model for evaluating the dataflow schedules
Distance $d_X(L)$
The number of loop iterations in the loop L , that separates two consecutive accesses to the same data element X
(d次iteration后,再也不会access到这次access的data element)
footprint $F_X(L_i)$
the footprint of array X in loop L measures the number of distinct elements of X used inside L.
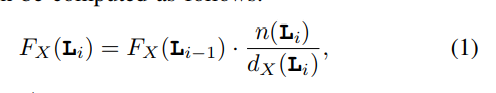
n(L) : loop L 的interation数目, L0 代表最里面的inner loop
the actual required size for the application-managed buffer is computed as follows:
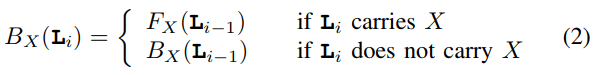
memory traffic $T_X$
number of bytes accessed in off-accelerator memory for array X
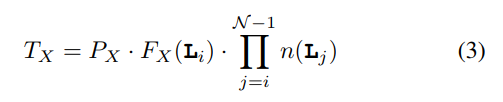
PX the numerical precision (in bytes) used for its storage.
It should be noticed that i here is actually defined on maximal B(Li) that fits the size of buffer